Link state routing is een techniek waarbij elke router de kennis van zijn buurt deelt met elke andere router in het internetwork.
De drie sleutels om het Link State Routing algoritme te begrijpen:
- Kennis over de buurt: In plaats van zijn routing tabel te zenden, zendt een router alleen de informatie over zijn buurt. Een router zendt zijn identiteiten en kosten van de direct verbonden links naar andere routers.
- Flooding: Elke router zendt de informatie naar elke andere router op het internetwerk behalve zijn buren. Dit proces staat bekend als Flooding. Elke router die het pakket ontvangt, zendt de kopieën naar al zijn buren. Tenslotte ontvangt elke router een kopie van dezelfde informatie.
- Informatie-uitwisseling: Een router zendt de informatie alleen naar elke andere router wanneer de verandering in de informatie optreedt.
Link State Routing kent twee fasen:
Reliable Flooding
- Initial state: Elk knooppunt kent de kosten van zijn buren.
- Eindtoestand: Elk knooppunt kent de hele grafiek.
Routeberekening
Elk knooppunt gebruikt Dijkstra’s algoritme op de grafiek om de optimale routes naar alle knooppunten te berekenen.
- Het Link state routing algoritme is ook bekend als Dijkstra’s algoritme dat wordt gebruikt om het kortste pad van een knooppunt naar elk ander knooppunt in het netwerk te vinden.
- Het Dijkstra’s algoritme is een iteratief, en het heeft de eigenschap dat na de k-de iteratie van het algoritme, de paden met de minste kosten goed bekend zijn voor k bestemmingsknooppunten.
Laten we enkele notaties beschrijven:
- c( i , j): Verbindingskosten van knooppunt i naar knooppunt j. Als de knooppunten i en j niet rechtstreeks met elkaar verbonden zijn, dan is c(i , j) = ∞.
- D(v): Het definieert de kosten van het pad van broncode naar bestemming v dat op dit moment de minste kosten heeft.
- P(v): Het definieert het vorige knooppunt (buur van v) samen met het huidige minst dure pad van bron naar v.
- N: Het is het totale aantal knooppunten dat beschikbaar is in het netwerk.
Algoritme
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
In het bovenstaande algoritme wordt een initialisatiestap gevolgd door de lus. Het aantal keren dat de lus wordt uitgevoerd, is gelijk aan het totale aantal knooppunten in het netwerk.
Laten we dit aan de hand van een voorbeeld begrijpen:
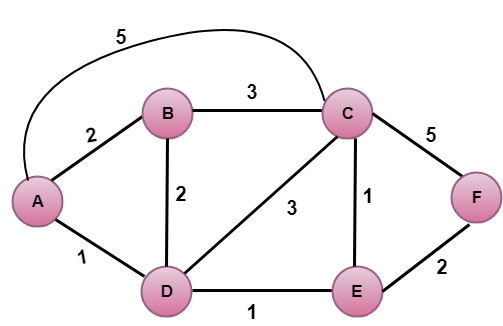
In de bovenstaande figuur is het bronpunt A.
Stap 1:
De eerste stap is een initialisatiestap. Het momenteel bekende minst gekoste pad van A naar zijn direct aangrenzende buren, B, C, D zijn respectievelijk 2,5,1. De kosten van A naar B worden op 2 gezet, van A naar D op 1 en van A naar C op 5. De kosten van A naar E en F worden op oneindig gezet, omdat ze niet direct met A verbonden zijn.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Step 2:
In bovenstaande tabel zien we dat vertex D het minst kostbare pad in stap 1 bevat. Daarom is het toegevoegd in N. Nu moeten we een minst-kosten pad bepalen door vertex D.
a) Kortste pad berekenen van A naar B
b) Kortste pad berekenen van A naar C
c) Kortste pad berekenen van A naar E
Noot: Het vertex D heeft geen directe link met vertex E. Daarom is de waarde van D(F) oneindig.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | 2 | AD | 2,A | 4,D | 2,D | ∞ |
Step 3:
In de bovenstaande tabel zien we dat zowel E als B het minst kostbare pad in stap 2 hebben. Laten we het E hoekpunt beschouwen. Nu bepalen we het minst gekoste pad van de overblijvende hoekpunten door E.
a) Berekening van het kortste pad van A naar B.
b) Berekening van het kortste pad van A naar C.
c) Berekening van het kortste pad van A naar F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | 2 | AD | 2,A | 4,D | 2,D | ∞ |
| 3 | ADE | 2,A | 3,E | 4,E |
Step 4:
In de bovenstaande tabel zien we dat B vertex het minst kostbare pad heeft in stap 3. Daarom wordt het toegevoegd in N. Nu bepalen we het minst gekoste pad van de overblijvende hoekpunten door B.
a) Berekening van het kortste pad van A naar C.
b) Berekening van het kortste pad van A naar F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E |
Stap 5:
In de bovenstaande tabel zien we dat C vertex het minst kostbare pad heeft in stap 4. Daarom wordt het toegevoegd in N. Nu bepalen we het minst gekoste pad van de overblijvende hoekpunten door C.
a) Berekening van het kortste pad van A naar F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| 5 | ADEBC | 4,E |
Eindtabel:
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E | |||
| 5 | ADEBC | 4,E | ||||
| 6 | ADEBCF |
Nadeel:
Zwaar verkeer wordt gecreëerd in Line state routing als gevolg van Flooding. Flooding kan een oneindige looping veroorzaken, dit probleem kan worden opgelost door gebruik te maken van Time-to-leave veld
