Een standaardafwijking is een getal dat ons vertelt
in welke mate een reeks getallen uit elkaar liggen.Een standaardafwijking kan variëren van 0 tot oneindig. Een standaardafwijking van 0 betekent dat een lijst getallen allemaal gelijk zijn – ze liggen helemaal niet uit elkaar.
Standaardafwijking – Voorbeeld
Vijf sollicitanten deden een IQ-test als onderdeel van een sollicitatie. Hun scores op drie IQ-componenten zijn hieronder weergegeven.
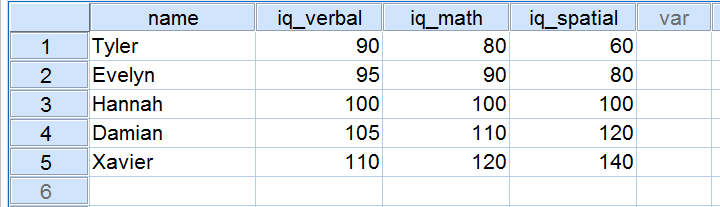
Nu gaan we de scores op de drie IQ-componenten eens onder de loep nemen. Merk op dat alle drie een gemiddelde van 100 hebben over onze 5 aanvragers. De scores op iq_verbaal liggen echter dichter bij elkaar dan de scores op iq_wiskunde. Bovendien liggen de scores op iq_spatial verder uit elkaar dan de scores op de eerste twee componenten. De precieze mate waarin een aantal scores uit elkaar liggen, kan worden uitgedrukt in een getal. Dit getal staat bekend als de standaardafwijking.
Standaardafwijking – Resultaten
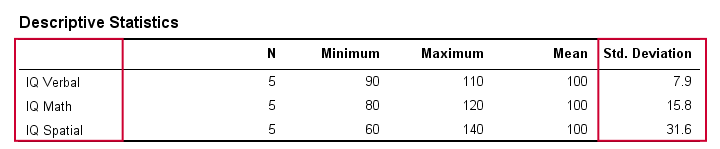
In het echte leven inspecteren we ruwe scores natuurlijk niet visueel om te zien hoe ver ze uit elkaar liggen. In plaats daarvan laten we ze berekenen door software (later meer daarover). De tabel hieronder toont de standaardafwijkingen en enkele andere statistieken voor onze IQ-gegevens. Merk op dat de standaardafwijkingen het patroon bevestigen dat we in de ruwe gegevens zagen.
Standaardafwijking en histogram
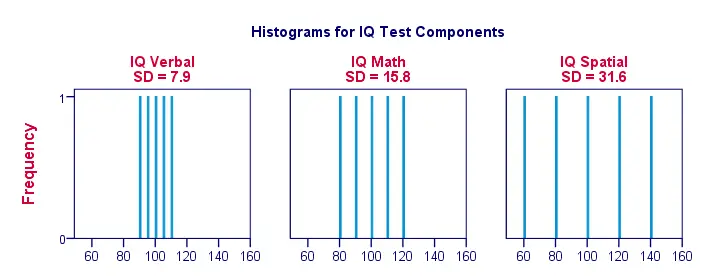
Rechter, laten we de dingen wat visueler maken. De figuur hieronder toont de standaardafwijkingen en de histogrammen voor onze IQ-scores. Merk op dat elke staaf de score van 1 kandidaat op 1 IQ component weergeeft. Opnieuw zien we dat de standaardafwijkingen aangeven in welke mate de scores uit elkaar liggen.
Standaardafwijking – meer histogrammen
Wanneer we gegevens over slechts een handvol observaties visualiseren, zoals in de vorige figuur, zien we gemakkelijk een duidelijk beeld. Voor een realistischer voorbeeld presenteren wij hieronder histogrammen voor 1.000 waarnemingen. Belangrijk is dat deze histogrammen identieke schalen hebben; voor elk histogram komt één centimeter op de x-as overeen met ongeveer 40 ‘IQ-componentpunten’.
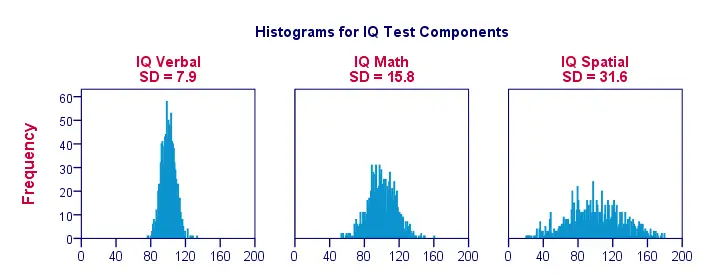
Merk op hoe de histogrammen ruwe schattingen van standaardafwijkingen mogelijk maken. “Bredere” histogrammen wijzen op grotere standaardafwijkingen; de scores (x-as) liggen verder uit elkaar. Aangezien alle histogrammen een identieke oppervlakte hebben (overeenkomend met 1000 waarnemingen), gaan hogere standaardafwijkingen ook gepaard met ‘lagere’ histogrammen.
Standaardafwijking – Populatieformule
Hoe berekent uw software dus standaardafwijkingen? Wel, de basisformule is
$$$$$$$$$
waar
- (X) elk afzonderlijk getal aanduidt;
- (X) staat voor het gemiddelde over alle getallen en
- (\sum) staat voor een som.
Met andere woorden, de standaardafwijking is de vierkantswortel uit het gemiddelde gekwadrateerde verschil tussen elk individueel getal en het gemiddelde van deze getallen.
Belangrijk is dat deze formule veronderstelt dat uw gegevens de gehele populatie van belang bevatten (vandaar “populatieformule”). Als uw gegevens slechts een steekproef uit uw doelpopulatie bevatten, zie hieronder.
Populatieformule – Software
U kunt deze formule gebruiken in Google sheets, OpenOffice en Excel door =STDEVP(...) in een cel te typen. Geef tussen de haakjes de getallen op waarover u de standaardafwijking wilt hebben en druk op Enter. De onderstaande figuur illustreert het idee.
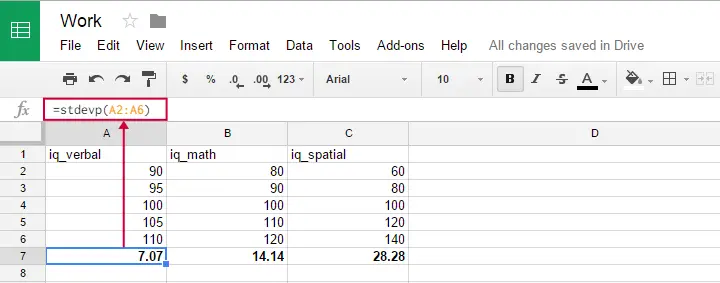
Opvallend genoeg lijkt de formule voor de standaardafwijking van de populatie niet te bestaan in SPSS.
Standaardafwijking – steekproefformule
Nu iets uitdagends: als uw gegevens (ongeveer) een eenvoudige aselecte steekproef zijn uit een (veel) grotere populatie, dan zal de vorige formule de standaardafwijking in deze populatie systematisch onderschatten. Een onvertekende schatter voor de standaardafwijking van de populatie wordt verkregen met
$$S_x = \sqrt{[X – \overline{X}]^2}{N -1}}$
Wat berekeningen betreft, is het grote verschil met de eerste formule dat we delen door \(n -1) in plaats van door \(n). Delen door een kleiner getal levert een (iets) grotere uitkomst op. Dit compenseert precies de eerder genoemde onderschatting. Voor grote steekproefgroottes hebben de twee formules echter vrijwel identieke uitkomsten.
In GoogleSheets, Open Office en MS Excel gebruikt de functie STDEV deze tweede formule. Het is ook de (enige) standaarddeviatieformule die in SPSS is geïmplementeerd.
Standaarddeviatie en Variantie
Een tweede getal dat uitdrukt hoe ver een verzameling getallen uit elkaar ligt, is de variantie. De variantie is de gekwadrateerde standaardafwijking. Dit impliceert dat, net als de standaardafwijking, de variantie zowel een populatie- als een steekproefformule heeft.
In principe is het onhandig dat twee verschillende statistieken in wezen dezelfde eigenschap van een verzameling getallen uitdrukken. Waarom laten we de variantie niet gewoon weg ten gunste van de standaardafwijking (of omgekeerd)? Het basisantwoord is dat de standaardafwijking in sommige situaties meer wenselijke eigenschappen heeft en de variantie in andere.
