Het schatten van tijd, inspanningen en kosten is een van de meest kritische onderdelen van projectmanagement. Dit komt door het fundamentele belang van deze schattingen voor de gehele projectplanning en, in het bijzonder, de reikwijdte, planning en kostenbasislijn. Een van de schattingstechnieken die in de PMI Project Management Body of Knowledge (PMBOK 6th ed., ch. 6.4, 7.2) worden voorgesteld, is de driepuntsschatting die wordt gebruikt met de driehoeks-, Beta- of PERT-verdeling. Wij zullen deze methoden in dit artikel introduceren.
Wat is de driepuntsschattingstechniek?
De driepuntsschatting is een eenvoudige maar nuttige benadering voor het schatten van de tijd of kosten van werkitems. Volgens de PMI methodologie wordt het gebruikt in de procesgroepen “Estimate Activity Duration” en “Estimate Costs”. De techniek omvat drie verschillende schattingen die gewoonlijk worden verkregen van materiedeskundigen:
- Optimistische schatting,
- Pessimistische schatting,
- Moedst waarschijnlijke schatting.
De optimistische schatting is de verwachte hoeveelheid werk of tijd die nodig is om een activiteit uit te voeren in de veronderstelling dat er geen belemmeringen optreden en dat alles soepel verloopt. Het vertegenwoordigt het zogenaamde best-case scenario. Het pessimistische punt is gebaseerd op de veronderstelling dat het tegenovergestelde waar is – het vertegenwoordigt het slechtst denkbare scenario. Hoewel beide schattingen betrekking hebben op de uiterste punten van het bereik van de verwachte uitkomsten, worden de schattingen geacht enigszins realistisch te zijn.
Het derde punt geeft het meest waarschijnlijke geval weer, het is de schatting van het werk of de tijd die als het meest realistisch wordt beschouwd. Men zou in de verleiding kunnen komen om gewoon het gemiddelde tussen het optimistische en het pessimistische punt te gebruiken zonder er verder over na te denken. Dit kan echter in veel gevallen niet geschikt zijn. In de praktijk loont het gewoonlijk de moeite om deze meest waarschijnlijke schatting goed te bepalen, analoog aan de andere schattingspunten.
Het resultaat van driepuntsschatting is een zogenaamde driehoeksverdeling van tijdswaarden of kostenbedragen, bestaande uit de drie schattingen (zie onderstaande illustratie).
Wat is PERT?
PERT staat voor Program Evaluation and Review Technique en werd ontwikkeld als een geavanceerd project planning en management systeem door de Amerikaanse marine in de jaren 1950 (bron: Heldman, PMP Study guide, ch. 4).
Een ander, niet al te serieus, verhaal over het ontstaan ervan werd ooit gepubliceerd door een anonieme auteur in PMI’s tijdschrift (Link; bron: Anoniem (1975). PERT-the hoax of the century. Project Management Quarterly, 6(3), 22-23).
In PMI-stijl projecten, wordt PERT voornamelijk gebruikt als een aanvullende techniek op de Kritische Pad Methode voor het plannen van activiteiten. Het kan echter ook worden toegepast op op zichzelf staande schattingen van werkitems en activiteiten.
De zogenaamde PERT-verdeling maakt gebruik van de waarden die zijn bepaald met de driepuntsschattingstechniek. Zij kan in principe worden gebruikt voor alle planningsniveaus, variërend van activiteiten tot volledige projecten. Het vinden van de juiste granulariteit voor zinvol schatten kan echter enig kritisch en conceptueel denken vereisen.
De PERT-methode impliceert het overwegen van de “meest waarschijnlijke” schatting. Zij zet de driepuntsschatting om in een klokvormige curve en maakt het mogelijk om waarschijnlijkheden van reeksen van verwachte waarden te bepalen.
Wat zijn de verschillen tussen de driehoeksverdeling en de PERT-verdeling van driepuntsschattingen?
Wanneer de driehoeksverdeling alleen de drie geschatte punten beschouwt, maakt de PERT-methode het mogelijk om de driepuntsschatting om te zetten in een klokvormige, bijna normaal verdeelde curve.Zij kan dus worden gebruikt voor de berekening van waarschijnlijkheden van reeksen van verwachte dalingen.
Het volgende diagram illustreert de verschillen tussen de PERT-verdeling, de driehoeksverdeling en de voorstelling van de driepuntsschatting als ware het een normale verdeling.
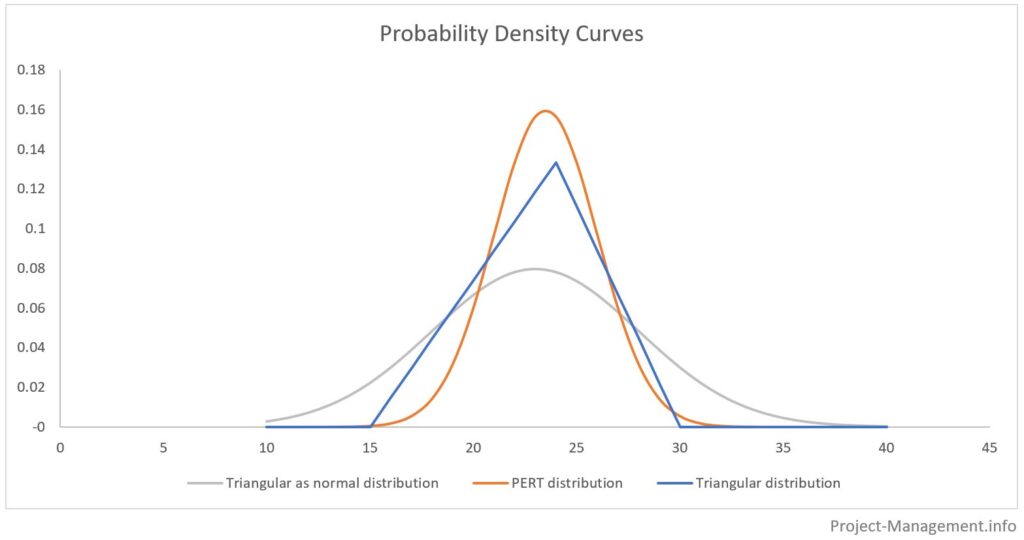
De gebieden onder de kansverdelingscurven geven de cumulatieve waarschijnlijkheid van de respectieve schattingsbereiken weer. Gewoonlijk worden deze bereiken bepaald met de verwachte waarde +/- standaardafwijking, vermenigvuldigd met 1, 2 en 3. Dit wordt geïllustreerd in de volgende figuur:
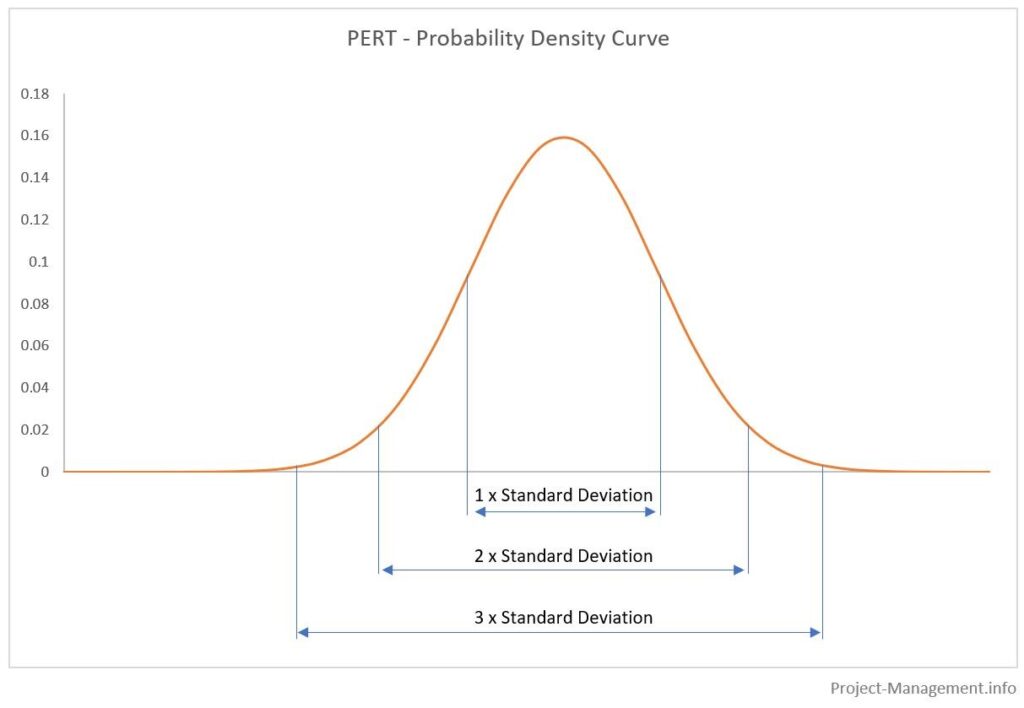
De resulterende waarschijnlijkheden (bij benadering) zijn
- 68,3% voor 1 standaardafwijking,
- 95.5% voor 2 standaardafwijkingen,
- 99,7% voor 3 standaardafwijkingen.
De vereiste kennis voor het PMP-examen beperkt zich tot het berekenen van de verwachte schattingen en het bekend zijn met de verschillende waarschijnlijkheden (bron). Daarom zullen wij de statistische details en achtergrond in dit artikel niet behandelen – u kunt die details vinden op Riskamp.
Gebruik deze calculator om de driepuntsschattingen en PERT te bepalen.
Hoe wordt de driepuntsschatting berekend?
De driehoeksverdeling
De eenvoudige maar veelgebruikte berekening omvat het gemiddelde of gemiddelde van de 3 geschatte waarden. De formule van deze driehoeksverdeling is:
E =(O + M + P) / 3
waar:
E = Verwachte hoeveelheid tijd of kosten,
O = Optimistische schatting,
M = Meest waarschijnlijke schatting,
P = Pessimistische schatting.
De PMBOK gebruikt t(E), t(O), t(M) en t(P) alsvariabelen voor tijdsschattingen en c(E), c(O), c(M) en c(P).
Het gewicht van elke schatting in deze vergelijking is identiek. Het “meest waarschijnlijke” geval heeft dus niet meer invloed op de uiteindelijke schatting dan de 2 minder waarschijnlijke schattingen. Dit verschilt van de methode van de bètaverdeling.
De PERT-bètaverdeling
De PERT-bètaverdeling houdt er rekening mee dat het “meest waarschijnlijke” geval waarschijnlijker is, hetgeen tot uiting komt in een multiplicator voor die schatting. De PMI-methodologie stelt deze berekening voor als alternatief voor de driehoeksverdeling voor kostenramingen (wij zijn echter van mening dat zij ook kan worden gebruikt voor tijdsramingen).
In deze methode krijgt de meest waarschijnlijke raming een vermenigvuldigingsfactor van 4, terwijl de totale deler wordt verhoogd tot 6. De formule is als volgt:
E =(O + 4*M + P) / 6
waar:
E = Verwachte hoeveelheid tijd of kosten,
O = Optimistische schatting,
M = Meest waarschijnlijke schatting,
P = Pessimistische schatting.
De standaardafwijking van de PERT-verdeling wordt berekend met de formule:
Standaardafwijking = (P – O) / 6
Voor het schatten van een volledig pad (analoge kritieke padmethode) wordt een soortgelijk concept toegepast, maar dan met gebruikmaking van een gecombineerde standaardafwijking van alle activiteiten.
Voorbeeld van een driepuntsschatting en PERT
Een team van materiedeskundigen schat de tijd die nodig is om een activiteit te voltooien. In dit voorbeeld wordt de duur van een activiteit geschat met behulp van de driepuntsschattingstechniek.Zij komen tot de volgende getallen:
| Optimistische schatting | 15 dagen |
| Pessimistische schatting | 24 dagen |
| Meest waarschijnlijke schatting | 30 dagen |
De waarden lopen uiteen van 15 dagen (optimistisch) tot 30 dagen (pessimistisch). Een duur van 24 dagen wordt het meest waarschijnlijk geacht voor de voltooiing van de werkzaamheden.
Berekening van de verwachte duur met een driehoeksverdeling
De verwachte duur met een driehoeksverdeling wordt als volgt berekend:
Eindschatting = (15 + 30 + 24) / 3.
De uiteindelijke schatting volgens deze methode is 23, wat in feite het ongewogen gemiddelde is van de drie schattingen.
Berekening van de verwachte duur met behulp van de bèta-verdeling van PERT
De verwachte duur kan ook worden berekend met de PERT-methode:
Eindschatting (verwachte waarde) = (15 + 4×24 + 30) / 6.
De verwachte waarde die hieruit voortvloeit is 23,5 dagen, wat meer is dan de eindschatting die met de driehoeksmethode is verkregen. Dit komt door het hogere gewicht (d.w.z. de vermenigvuldigingsfactor 4) die aan de “meest waarschijnlijke” schatting wordt toegekend.
De standaardafwijking van deze schatting is:
Standaardafwijking = (30 – 15) / 6 = 2,5
Bepaling van de waarschijnlijkheid van de verwachte duur
Na berekening van de verwachte duur en de standaardafwijking kan de projectmanager de waarschijnlijkheid (bij benadering) bepalen:
.):
| Bereik | Waarschijnlijkheid | Ondergrens | Bovengrens |
| 1 x standaardafwijking | 68.3% | 21 | 26 |
| 2 x standaardafwijking | 95.5% | 18,5 | 28,5 |
| 3 x standaardafwijking | 99.7% | 16 | 31 |
Met 68,3% waarschijnlijkheid zal de duur van de activiteit tussen 21 en 26 dagen liggen. Voor een bereik van 18,5 tot 28,5 dagen is de waarschijnlijkheid 95,5%. Het gebruik van 3 standaardafwijkingen dekt bijna alle datapunten en geeft een waarschijnlijkheid van 99,7% dat de duur uiteindelijk tussen 16 en 31 dagen zal liggen.
Samenvatting
De uiteindelijke schatting volgens de driehoeksmethode was 23, vergeleken met 23,5 volgens de PERT-methode. Dit komt doordat de laatste een groter gewicht toekent aan het “meest waarschijnlijke” geval, dat in ons geval niet precies het gemiddelde (of ongewogen gemiddelde) is van de optimistische en de pessimistische schatting.
Met behulp van de PERT-methode kan rekening worden gehouden met waarschijnlijkheden van waardebereiken. Dit is nuttig als de kwaliteit van de ramingen varieert, bijvoorbeeld als het verschil tussen optimistische en pessimistische ramingen aanzienlijk afwijkt tussen verschillende activiteiten. In dat geval zal het gebruik van ranges en hun waarschijnlijkheden de spreiding en het betrouwbaarheidsniveau van de onderliggende schattingen weergeven.
Conclusie
De schatting van activiteiten met betrekking tot hun tijd- en kostenvereisten is van cruciaal belang voor de planning en roostering van projecten en activiteiten. In veel projecten zijn meer nauwkeurige schattingen, zoals parametrische schattingen, gebaseerd op statistische correlaties van vergelijkbare projecten in het verleden, niet beschikbaar. De driepuntsschattingstechniek biedt een goede benadering voor het verwerken en in evenwicht brengen van top-down of subject matter expert schattingen in dergelijke situaties.
De PERT-verdeling is waarschijnlijk de meest nauwkeurige methode om deze slechtste, beste en meest waarschijnlijke gevallen samen te voegen tot een enkel cijfer (verwachte waarde) of een reeks van waarden. Dankzij het gebruik van de standaardafwijking wordt rekening gehouden met zowel de inherente onzekerheden als de mogelijke verstrooiing van de schattingen.
Dit zou de reden kunnen zijn waarom PERT nog steeds een veelgebruikte methode is voor het schatten en roosteren van projecten, hoewel deze al enkele decennia bestaat en al door onze grootouders had kunnen worden gebruikt (als zij projectmanagers waren geweest).
