Toepassing van de stelling van Buckingham Pi

Volgende: Belang van Niet-Dimensionale Getallen Up: Buckingham Pi Stelling Previous: Buckingham Pi Stelling

Toepassing van Buckingham Pi stelling

De stelling die we hebben gesteld is zeer algemeen, maar geenszins beperkt tot de Vloeistofmechanica. Zij wordt gebruikt op verschillende gebieden zoals plantkunde en sociale wetenschappen en er zijn boeken en boekdelen over dit onderwerp geschreven. Maar we hebben niet veel theorie nodig om het te kunnen toepassen. Wat we zullen overwegen is een procedure om de stelling te gebruiken en te komen tot niet-dimensionale getallen voor een gegeven stroming.

1. Lijst alle variabelen die het proces bepalen. Deze variabelen moeten onafhankelijk van elkaar zijn. Men moet bijvoorbeeld niet de dichtheid, de zwaartekracht en het soortelijk gewicht kiezen. Dichtheid en soortelijk gewicht moeten volstaan. Voor ons probleem hebben we F, D, V, en . We hebben n = 5.
2. Markeer de herhalende variabelen. In ons geval zijn dat D, V en waardoor k = 3.
3. Bepaal hoeveel niet-dimensionale getallen er zijn. Voor ons geval hebben we n – k = 2. Ons probleem heeft 2 niet-dimensionale getallen, en .
4. Definieer de niet-dimensionale getallen door de variabelen te groeperen in n – k groepen zodat elke groep alle herhalende variabelen heeft en één niet-herhalende variabele. Voor ons probleem hebben we dus

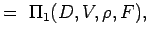
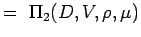
   		(5.2)
   Let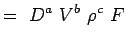
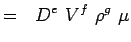
   		(5.3)

5. Denk nu elke variabele uit te drukken in termen van zijn afmetingen. Laten we het MLT-systeem gebruiken volgens hetwelk de variabelen voor onze problemen de volgende dimensies hebben.
   

   Variabele	Dimensies
   F, Kracht	M L / T2 of M L T-2
   D, Diameter:	L
   V, Snelheid	L/T of LT-1
   , Dichtheid:	M/L3 of ML-3
   , Viscositeit	ML-1T-1

   Substitueren we deze dimensies in Eqn. 5.2, hebben we

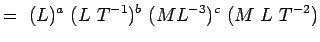
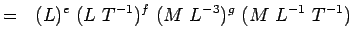
   		(5.4)
   Or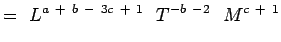
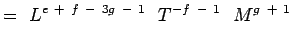
   		(5.5)

   Noemend dat en niet-dimensionaal zijn hebben we,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Oplossen van de vergelijkingen levert op,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Nu worden onze niet-dimensionale getallen,

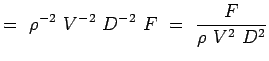
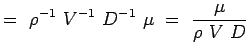
   		(5.8)

Hiermee hebben we de niet-dimensionale getallen gevonden voor de stroming waar het om gaat, namelijk de weerstand om een cirkelvormige cilinder. De functionele relatie tussen de twee getallen kan worden uitgedrukt als

Maar merk op dat de vorm van term die we hebben afgeleid enigszins verschilt van wat we in het begin aannamen. De rechterzijde van de vergelijking is in feite het omgekeerde van het getal van Reynolds! Dit wijst op het nadeel van de analyse dat de exacte functionele vorm tussen de getallen niet kan worden verkregen. Elke coëfficiënt of index die wordt verkregen kan niet door deze analyse worden bepaald. Dit moet worden bepaald door experimenten of door berekeningen. Maar aangezien de getallen niet-dimensionaal zijn, kunnen we kanaalwegen schrijven,

Volgende: Belang van niet-dimensionale getallen Up: Buckingham Pi Theorema Previous: Buckingham Pi Theorema

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
Universiteit van Sydney